back
Finding gaps in a sequence of identifier values of sql table.
By Mirek on (tags: gaps in sequence, id gap, table id finding, categories: code)Today I would like to present a couple of solutions for problem of finding gap in a sequence. This issue will be considered in context of finding missing – gap identifiers in the database table. All examples of code are T-SQL scripts and statements and were tested on SQL Server 2008 Express
1. Integer typed identifiers
Lets assume we have an sql table with following schema
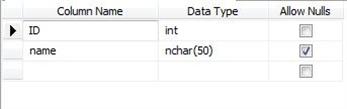Field ID is the unique key identity key of the table which holds integers. Other fields are not important for the purposes of this article. The assumption is that the ID sequence starts from 1.
Additionally there is an unique no clustered index founded on the ID field, which will hold all ID’s of the table in ascending order. This is generally a desirable technique to have an index on table identity columns which drastically improves searching process over indexed table.
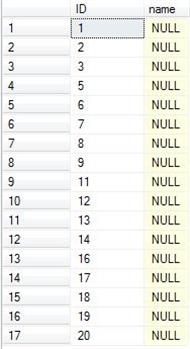
Lets now assume the table was field with a 20 records and after that some of the records were deleted
As you can see there is lack of ID: 4, 10 and 15. The challenge is to find these ID’s and reuse them when inserting new rows into the table. Moreover this operation should be performed in a minimum time so do not affect insert operations and do not block the table. After search the internet resources and some self investigation I came into few solutions which I wanted to choose the best one.
I will try to focus on finding first free ID at first and below is the list of tsql implementations to find so.
Tested table is named ITable_6 and has an ID field of type int.
1. Naive approach
The naive approach relays on one by one checking the ID’s existence in the table. Following is the tsql implementation of this solution.
1: begin
2: declare @iterator int;
3: declare @mcount int;
4:
5: set @mcount = (select count(*) from ITable_6);
6:
7: set @iterator = 0;
8:
9: while @iterator < @mcount
10: begin
11: set @iterator = @iterator +1;
12: if not exists(select null from ITable_6 where ID = @iterator)
13: break;
14: end;
15:
16: select @iterator;
17:
18: end;
The iterator goes from 1 to count of the table and in each iteration checks the existence of the ID. If particular ID does not exists in the table then it is returned as found gap ID.
2. Using ‘NOT EXISTS’ operator
This solution is based on checking if every identity value has its successor in the table and returning this successor if it does not exists. The disadvantage is that the first identity value 1 has to be checked manually as long as it is not a successor of any positive integer so is not checked. The advantage is that if there are no gaps in the table then the next after maximum is returned automatically.
1: select a.ID+1 from ITable_6 a
2: where not exists (select * from ITable_6 b
3: where a.ID+1 = b.ID)
4: order by a.ID
3. In memory sequence table
Generally an approach to find a gap in a sequence of numbers (identifiers in this case) is to compare this sequence to the set of natural numbers. In case of table identifiers we can compare it to the set of positive integers, which is obviously a natural comparison.
The ideal situation would be that if we have for instance n rows in the table then the identifiers are in range from 1 to n. So to find the gaps in the table we must construct the numbers sequence from 1 to the count of the table and compare it together checking which number from the numbers sequence does not exists in the examined table.
1: declare @numbers table (n int not null);
2: declare @idx int;
3: declare @cnt int;
4: select @cnt = count(*) from ITable_6;
5: set nocount on ;
6: set @idx=1;
7: while @idx < (@cnt+1)
8: begin
9: insert @numbers values (@idx) ;
10: set @idx=@idx+1;
11: end;
12: set nocount off;
13:
14: elect N.n
15: from @numbers as N
16: where not exists (select null from ITable_6 b
17: where N.n = b.ID)
18: order by N.n;
This is generally not efficient solution. Especially for a tables with big amount of rows the generation of the sequence table may take a long time.
4. Sequence numbers using ROW_NUMBER()
Another approach is to use a numbers of rows of the table as a ready for use sequence of the ascending numbers. The requirement is that the values has to be sorted in ascending order. Now if we assume that there is ID equal 1 in row number 1, ID equal 2 in row number 2 and so on then we can easily find the first gap ID. The first row number which contains ID value greater that row number, is the actual first gap ID.
1: select top 1 RN from
2: (select ID, row_number() over (order by ID) as RN
3: from ITable_6) as T
4: where ID > RN
Look again at a second picture in this article presenting the table with row numbers and ID values. In row number 4 the ID value equals 5 so the first gap ID is 4. As you can see this statement returns only a first element because all others are useless in this case.
5. Using CURSOR and ‘Divide and Conquer’
Extending approach 4. we can improve it by using Divide and conquer algorithm. This relays on dividing the scope of the problem into two parts and processing each of these parts separately. Then treating each of parts as new problem scope using algorithm recursively.
We will take for example our table shown on picture 2.
The algorithm here will go in following steps:
- Check the center of the rows set; it is row number 8 and contains and ID with value 9, which means the gap ID resides in the first/left part of the rows set. Remember 8 as last found ID.
- Check the rows from 1 to 8.
- Check the center of the rows set; it is row number 4 and contains and ID with value 5, which means the gap ID resides in the first/left part of the rows set. Remember 4 as last found ID.
- Check rows from 1 to 4
- Check the center of the rows set; it is row number 2 and contains and ID with value 2, which means the gap ID resides in the right part of the rows set.
- Check row 3; it contains ID with value 3, which means the gap ID resides in the right part of the rows set.
- Set length is 1 so the result is last found ID = 4
This approach limits the count of fetched values to minimum.
1: CREATE PROCEDURE [GetTableIDInt] (@TableName varchar(100),
2: @FieldName varchar(100), @ResultID int OUTPUT)
3: AS
4: BEGIN
5: --cursor navigation
6: DECLARE @currentRowNo int; --current iteration row number
7: DECLARE @leftLimit int; --number of left bound row
8: DECLARE @rightLimit int; --number of right bound row
9: DECLARE @rowCount int; --total rows returned by cursor
10:
11: --ID parsing
12: DECLARE @currentId int; --ID value fetched and parsed from current row
13: DECLARE @lastFoundId int; --last found gap ID
14: DECLARE @query nvarchar(500); --main iterator query
15: DECLARE @iditerator CURSOR; --main iterator of the Ids
16:
17: SET @ResultID = 0;
18:
19:
20: -- construct a query which declares and opens the cursor;
21: SET @query = N'SET @cursor = CURSOR SCROLL READ_ONLY FOR
22: SELECT '+@FieldName+'
23: FROM ['+@TableName+']
24: WITH (TABLOCKX) ORDER BY '+@FieldName+' OPEN @cursor ';
25:
26: EXECUTE sp_executesql @query, N'@cursor cursor output', @iditerator output;
27:
28: -- initial fetch useless but necessary
29: FETCH LAST FROM @iditerator INTO @currentId;
30:
31: --get the number of rows affected by the cursor
32: SET @rowCount = @@CURSOR_ROWS;
33:
34: --prepare initial search limits
35: SET @leftLimit = 1;
36: SET @rightLimit = @rowCount;
37: SET @currentRowNo = 0;
38: SET @lastFoundId = 0;
39:
40:
41: IF (@currentId > @rowCount)
42: BEGIN
43: --iterate with Divide and Conquer algorithm
44: WHILE (@leftLimit<@rightLimit) AND (@@FETCH_STATUS = 0)
45: BEGIN
46: --resolve special case when limits are next to each other
47: if ((@rightLimit - @leftLimit) = 1)
48: BEGIN
49: --check left side row
50: FETCH ABSOLUTE @leftLimit FROM @iditerator INTO @currentId;
51: IF (@currentId > @leftLimit)
52: BEGIN
53: SET @lastFoundId = @leftLimit;
54: BREAK;
55: END;
56: --check right side row
57: FETCH ABSOLUTE @rightLimit FROM @iditerator INTO @currentId;
58: IF (@currentId > @rightLimit)
59: BEGIN
60: SET @lastFoundId = @rightLimit;
61: BREAK;
62: END;
63: --break all recursion - no ID gaps found
64: BREAK;
65: END;
66:
67: --find the middle row number of the range
68: SET @currentRowNo = FLOOR((@rightLimit + @leftLimit) / 2);
69: --and take its ID value
70: FETCH ABSOLUTE @currentRowNo FROM @iditerator INTO @currentId;
71:
72: --if ID is greater than row number we have to check/iterate left
73: --subset of the results
74: IF (@currentId > @currentRowNo)
75: BEGIN
76: --remember this as found ID
77: SET @lastFoundId = @currentRowNo;
78: SET @rightLimit = @currentRowNo;
79: CONTINUE;
80: END
81: ELSE --elsewhere we check the right half of the range
82: BEGIN
83: SET @leftLimit = @currentRowNo;
84: CONTINUE;
85: END;
86:
87: END; -- end of main WHILE iteration
88: END;
89:
90: --if no free id found then the table has no gaps
91: --get the next from the maximum row number
92: IF (@lastFoundId = 0)
93: SET @ResultID = @rowCount + 1;
94: ELSE
95: SET @ResultID = @lastFoundId;
96:
97: CLOSE @iditerator;
98: DEALLOCATE @iditerator;
99:
100: END
6. Using sql self LEFT JOIN
This approach is based on joining the table to its self with left join and comparing left table ID value with right table ID + 1 value. This method can be used to return only first gap ID. Since this statement always returns an ID + 1 value and iterates from 1 so it is un able to detect the gap at position 1. To fix that an additional select statement is performed, see line 7.
1: select top 1 p.id + 1
2: from ITable_6 as p
3: left join ITable_6 as alt
4: on alt.id = p.id + 1
5: where alt.id is null
6: union
7: select 1 where not exists (select null from ITable_6 where id=1)
Ok lets test this stuff a little. I have generated a table with 2 000 000 IDs and remove the 1999999 ID. So the table contains 1 999 999 IDs and the test consist on finding first gap id which is the removed one.
| Sequence numbers using ROW_NUMBER() | 553 ms |
| Using ‘NOT EXISTS’ operator | 880 ms |
| LEFT JOIN approach | 1070 ms |
| Using CURSOR and ‘Divide and Conquer’ | 3993 ms |
| Naive approach | 21016 ms |
| In memory sequence table | 47286 ms |
2. String typed identifiers with preffix and suffix
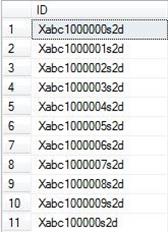
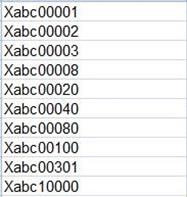
Now lets extend our table so it contains an string based identifiers instead of int values. Moreover let’s assume that we can hold many kinds of set of identifiers which will be distinguished by prefix and suffix. ID is build in following form: [Prefix][ID value][Suffix]
Above table contains the ids combined with prefix Xabc and suffix s2d. All approaches must be adopted to support this kind of complication.
First obvious conclusion is now that the performance will drastically decrease, since each value must be parsed and number must be extracted from it. Moreover the unique ascending index is less useful here now since sorting string representation of the numbers is not the same as sorting numbers.
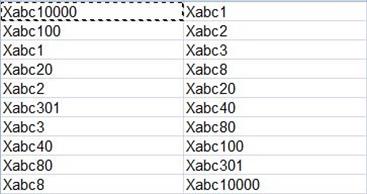
Below you can see: in the left column string based sorting and in the right column values sorted by its numeric part value. (The suffix was removed for clarity)
This issue would be fixed by complementing the numbers with zeros so the each value has the same length
Unfortunately we can not assume the fixed length of the value, since this value can grow so the number representation will exceed the length of the previous values (here ex. Xabc100001).
To extract the numeric values from the table the following statement is useful
1: select CID = CAST(STRID as int)
2: from
3: (
4: select STRID = SUBSTRING(ID,4 + 1, LEN(ID) - 4 - 3)
5: from [Test] (UPDLOCK)
6: where (ID LIKE 'Xabc%s2d')
7: ) as T
8: where (ISNUMERIC(STRID) = 1)
9: order by CID
It actually returns sorted ascending integer values extracted from the ID field. Notice that the only fields that match pattern [Prefix][value][Suffix] and for which inner [value] is a number representation. The value of SUBSTRING function is computed of the form: SUBSTRING(ID,@PrefixLength + 1, LEN(ID) - @PrefixLength - @SuffixLength).
UPDLOCK option assures that no one change the table until the result of the statement is retrieved. The difference with TABLOCKX option used here in previous implementations is that the UPDLOCK allows reading the table, while TABLOCKX is an exclusive lock for all CRUD operations.
Below are the updated implementations of four mentioned approaches adopted to support prefixed/suffixed ids. I have skipped the ‘In memory sequence table’ approach because of this obvious performance overhead.
Most of below implementations uses an in memory temporary table which is filled with actually parsed and sorted integer values from the main table string values. Then the implementation is used the same as for int based ID table.
1. Naive approach
1: begin
2: declare @iterator int;
3: declare @mcount int;
4:
5: set @mcount = (select count(*) from TwoMilions_Str)+1;
6:
7: set @iterator = 0;
8:
9: while @iterator < @mcount
10: begin
11: set @iterator = @iterator +1;
12: if not exists(select null from TwoMilions_Str (UPDLOCK)
13: where ID LIKE 'Xabc'+cast(@iterator as varchar(20)) +'s2d' )
14: break;
15: end;
16:
17: select @iterator;
18: end;
In line 5 I have added a ‘+1’ which now allows to find the next id in the table when there are no gaps.
2. Using ‘NOT EXISTS’ operator
1: begin
2:
3: declare @t table (ID int primary key);
4:
5: insert @t select CID = CAST(STRID as int)
6: from
7: (
8: select STRID = SUBSTRING(ID,4 + 1, LEN(ID) - 4 - 3)
9: FROM [TwoMilions_Str] (UPDLOCK)
10: WHERE (ID LIKE 'Xabc%s2d')
11: ) as T
12: where (ISNUMERIC(STRID) = 1);
13:
14: select RID = a.ID+1 from @t a
15: where not exists (select * from @t b where a.ID+1 = b.ID)
16: union select ResID = 1 where not exists (select null from @t where ID= 1)
17: order by RID;
18:
19: end;
Line 16 contains special case for gap in position 1 which is here explicitly checked.
3. Sequence numbers using ROW_NUMBER()
1: DECLARE @temp TABLE (CID int primary key);
2:
3: insert @temp select CID = CAST(STRID as int)
4: from
5: (
6: select STRID = SUBSTRING(ID,4 + 1, LEN(ID) - 4 - 3)
7: FROM [TwoMilions_Str] (UPDLOCK)
8: WHERE (ID LIKE 'Xabc%s2d')
9: ) as T0
10: where (ISNUMERIC(STRID) = 1);
11: select top 1 RN from
12: (
13: select CID, RN = row_number() over (order by CID) from @temp
14: union select MAX(CID)+2,MAX(CID)+1 from @temp
15: ) as T2
16: where (CID > RN);
4. Using CURSOR and ‘Divide and Conquer’
1: CREATE PROCEDURE [GetTableID] (@Prefix varchar(50),@Suffix varchar(50), @TableName varchar(100),
2: @FieldName varchar(100), @ResultID int OUTPUT)
3: AS
4: BEGIN
5: --cursor navigation
6: DECLARE @currentRowNo int; --current iteration row number
7: DECLARE @leftLimit int; --number of left bound row
8: DECLARE @rightLimit int; --number of right bound row
9: DECLARE @rowCount int; --total rows returned by cursor
10:
11: DECLARE @LenPrefix nvarchar(50);
12: DECLARE @LenSuffix nvarchar(50);
13:
14: --ID parsing
15: DECLARE @currentId int; --ID value fetched and parsed from current row
16: DECLARE @lastFoundId int; --last found gap ID
17: DECLARE @query nvarchar(1000); --main iterator query
18: DECLARE @iditerator CURSOR; --main iterator of the Ids
19:
20: SET @Prefix = COALESCE(@Prefix,'');
21: SET @Suffix = COALESCE(@Suffix,'');
22:
23: SET @LenPrefix = CAST(LEN(@Prefix) as nvarchar(50));
24: SET @LenSuffix = CAST(LEN(@Suffix) as nvarchar(50));
25:
26: SET @ResultID = 0;
27:
28: -- construct a query which declares and opens the cursor;
29: -- iterate the ID's, remove prefix, parse the numeric value and sort by these values
30: -- inner 2 nested select statements do following
31: --- select all values that match pattern [prefix]value[suffix] and extract the value
32: --- select only these values which represents number
33: SET @query = N'set @cursor = cursor scroll read_only for
34: select CID = cast(STRID as int)
35: from
36: (
37: select STRID = substring('+@FieldName+','+@LenPrefix +' + 1,
38: len('+@FieldName+') - '+@LenPrefix +' - '+@LenSuffix +')
39: from ['+@TableName+'] (UPDLOCK)
40: where ('+@FieldName+' like '''+@Prefix +'%'+@Suffix +''')
41: ) as T0
42: where (isnumeric(STRID) = 1)
43: order by CID
44: open @cursor ';
45:
46: EXECUTE sp_executesql @query, N'@cursor cursor output', @iditerator output;
47:
48: -- initial fetch; check the last one element
49: FETCH LAST FROM @iditerator INTO @currentId;
50:
51: --get the number of rows affected by the cursor
52: SET @rowCount = @@CURSOR_ROWS;
53:
54: --prepare initial search limits
55: SET @leftLimit = 1;
56: SET @rightLimit = @rowCount;
57: SET @currentRowNo = 0;
58: SET @lastFoundId = 0;
59:
60: --if last one ID value is not greater than row count
61: --then the table does not contain gaps in IDs
62: IF (@currentId > @rowCount)
63: BEGIN
64: --iterate with Divide and Conquer algorithm
65: WHILE (@leftLimit<@rightLimit) AND (@@FETCH_STATUS = 0)
66: BEGIN
67: --resolve special case when limits are next to each other
68: if ((@rightLimit - @leftLimit) = 1)
69: BEGIN
70: --check left side row
71: FETCH ABSOLUTE @leftLimit FROM @iditerator INTO @currentId;
72: IF (@currentId > @leftLimit)
73: BEGIN
74: SET @lastFoundId = @leftLimit;
75: BREAK;
76: END;
77: --check right side row
78: FETCH ABSOLUTE @rightLimit FROM @iditerator INTO @currentId;
79: IF (@currentId > @rightLimit)
80: BEGIN
81: SET @lastFoundId = @rightLimit;
82: BREAK;
83: END;
84: --break all recursion - no ID gaps found
85: BREAK;
86: END;
87:
88: --find the middle row number of the range
89: SET @currentRowNo = FLOOR((@rightLimit + @leftLimit) / 2);
90: --and take its ID value
91: FETCH ABSOLUTE @currentRowNo FROM @iditerator INTO @currentId;
92:
93: --if ID is greater than row number we have to check/iterate left
94: --subset of the results
95: IF (@currentId > @currentRowNo)
96: BEGIN
97: --remember this as found ID
98: SET @lastFoundId = @currentRowNo;
99: SET @rightLimit = @currentRowNo;
100: CONTINUE;
101: END
102: ELSE --elsewhere we check the right half of the range
103: BEGIN
104: SET @leftLimit = @currentRowNo;
105: CONTINUE;
106: END;
107:
108: END; -- end of main WHILE iteration
109: END;
110: --if no free id found then the table has no gaps
111: --get the next from the maximum row number
112: IF (@lastFoundId = 0)
113: SET @ResultID = @rowCount + 1;
114: ELSE
115: SET @ResultID = @lastFoundId;
116:
117: CLOSE @iditerator;
118: DEALLOCATE @iditerator;
119:
120: END
6. Using sql self LEFT JOIN
1: DECLARE @temp TABLE (ID int primary key);
2:
3: insert @temp select CAST(STRID as int)
4: from
5: (
6: select STRID = SUBSTRING(ID,4 + 1, LEN(ID) - 4 - 3)
7: FROM [TwoMilions_Str] (UPDLOCK)
8: WHERE (ID LIKE 'Xabc%s2d')
9: ) as T
10: where (ISNUMERIC(STRID) = 1);
11:
12: SELECT top 1 p.ID + 1
13: FROM @temp as p
14: LEFT JOIN @temp AS alt
15: ON alt.ID = p.ID + 1
16: WHERE alt.ID IS NULL
17: union
18: select 1 where not exists (select null from @temp where ID=1)
Tests
1. Finding gap id in 2000000 rows table at position 1
| Naive approach | 143 ms |
| Sequence numbers using ROW_NUMBER() | 13 183 ms |
| LEFT JOIN approach | 14 240 ms |
| Using ‘NOT EXISTS’ operator | 15 130 ms |
| Using CURSOR and ‘Divide and Conquer’ | 17 130 ms |
2. Finding gap id in 2000000 rows table at position 1999999
| Sequence numbers using ROW_NUMBER() | 13 976 ms |
| Using ‘NOT EXISTS’ operator | 14 556 ms |
| LEFT JOIN approach | 15 643 ms |
| Using CURSOR and ‘Divide and Conquer’ | 17 446 ms |
| Naive approach | 67 280 ms |
3. Finding the next free id in the table – no gaps in the table.
| Sequence numbers using ROW_NUMBER() | 13 950 ms |
| LEFT JOIN approach | 14 160 ms |
| Using ‘NOT EXISTS’ operator | 15 223 ms |
| Using CURSOR and ‘Divide and Conquer’ | 17 593 ms |
| Naive approach | 66 563 ms |
4. Finding all gaps in the table (gaps in position 1, 1000000 and 1999999)
| Using ‘NOT EXISTS’ operator | 15 630 ms |
| Using CURSOR and ‘Divide and Conquer’ | N/A |
| Sequence numbers using ROW_NUMBER() | N/A |
| LEFT JOIN approach | N/A |
| Naive approach | 65 360 ms |
3. Conclusion
To be honest the “Divide and conquer” approach was my favorite in this competition. Since it fetches only a small subset of all table IDs, it seems to be the most efficient algorithm. The bottle neck of all implementations was sorting values in ascending order. This was the most time and resource consuming operation. In case of integer type ID, very helpful here is an unique, non clustered index, which actually holds all IDs in ascending order sorted. In string based ID the main bottle neck is parsing the values and extracting number from string name.
If we need to find first free ID in the table we should use ROW_NUMBER() approach since it is the fastest for all cases. If we want to get the list of all gap ids we can use ‘NOT EXISTS’ approach which is only a slightly slower.
ROW_NUMBER() approach packed as a stored procedure below
1: CREATE PROCEDURE [GetTableID_ROWNUMBER] (@Prefix varchar(50),@Suffix varchar(50), @TableName varchar(100),
2: @FieldName varchar(100), @ResultID int OUTPUT)
3: AS
4: BEGIN
5: DECLARE @LenPrefix nvarchar(10);
6: DECLARE @LenSuffix nvarchar(10);
7: DECLARE @query nvarchar(1000);
8:
9: SET @Prefix = COALESCE(@Prefix,'');
10: SET @Suffix = COALESCE(@Suffix,'');
11:
12: SET @LenPrefix = CAST(LEN(@Prefix) as nvarchar(50));
13: SET @LenSuffix = CAST(LEN(@Suffix) as nvarchar(50));
14:
15: SET @ResultID = null;
16:
17:
18: -- construct main query
19: -- 4 nested selects do as follows:
20: --- select all values that match pattern [prefix]value[suffix] and extract the value
21: --- select only these values which represents number
22: --- select int value and row number ordered
23: --- select first ofv values which is greater than its row number
24: SET @query = N'DECLARE @temp TABLE (CID int primary key);
25:
26: insert @temp select CID = CAST(STRID as int)
27: from
28: (
29: select STRID = SUBSTRING('+@FieldName+','+@LenPrefix +' + 1,
30: LEN('+@FieldName+') - '+@LenPrefix +' - '+@LenSuffix +')
31: FROM ['+@TableName+'] (UPDLOCK)
32: WHERE ('+@FieldName+' LIKE '''+@Prefix +'%'+@Suffix +''')
33: ) as T0
34: where (ISNUMERIC(STRID) = 1);
35: select top 1 @ResultID = RN from
36: (
37: select CID, RN = row_number() over (order by CID) from @temp
38: union select MAX(CID)+2,MAX(CID)+1 from @temp
39: ) as T2
40: where (CID > RN);';
41:
42: EXECUTE sp_executesql @query, N'@ResultID int output', @ResultID output;
43:
44: END
Dejh
12/12/2013 1:10 PM
Just used the Not Exists approach very successfully. Many Thanks DavidShanthi
3/31/2014 12:14 PM
nice explanation... great article... :). Thanks for sharingThomas Abruzzo
1/13/2017 9:30 PM
Excellent! This helped me out big time today. We are using the in memory approach. Which works well because we have some ‘reserved’ values that we want to skip?Yakov
7/25/2019 11:56 AM
Thank to You. Helped me a lot.Storychanges.com
11/1/2024 3:44 AM
How do you see artificial intelligence revolutionizing the way we approach software development, testing, and maintenance in the near future? What are the potential risks and benefits of integrating AI into our workflows?", "refusal